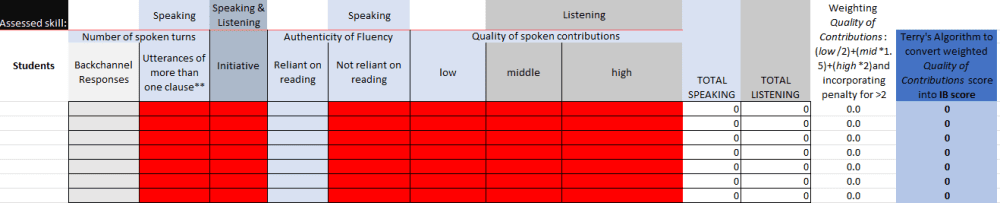
This article reports on the addition of two further columns to the Discussion Skills Assessment (DSA) instrument: Columns L and M as shown in the screenshot below.
I have been using the DSA to assess my IB MYP English Language and Literature (ELL) students during student-led seminar discussions in class. My previous research (Clark & Terrett, 2024) indicates that the DSA’s speaking and listening scores are consistent with existing standardised tests, but the open ended nature of the scoring system makes it tricky to convert the scores to an appropriate score out of 8 for the IB assessment criteria.
Another issue had been the fact that in ELL class, as with other disciplines that are not focused solely on language acquisition, the assessment criteria are not ‘speaking’ and ‘listening’, but rather include skills such as ‘analysing’ and ‘organising’. To accomodate this, I created an additional column (L) on the DSA instrument that resulted in a weighted score for the Quality of Contributions DSA criteria. This halved the low quality of contributions, multiplied the middle quality contributions by 1.5, and doubled the high. However, this score remained open-ended and still needed to be converted into an IB score out of 8.
One of my current students called Terry is acknowledged by his classmates to be a math whizz, and he is also keenly motivated by our recent seminar discussions analysing WWI poems. This led to him providing me with a formula to use for converting the weighted Quality of Contribution scores into IB assessment scores in one of his reflections on the seminar experience. The rationale and working are outlined below.
Incorporating Terry’s Formula
Here is the formula supplied by Terry (I hope this is correct, but must admit I struggled a bit with the handwriting):
f(x)=8⋅(1−c−0.5x)
Here, ‘c’ (the constant determining the rate of decay) is raised to the power of ‘-0.5x’ to function as an exponential decay to adjust the input numbers.
To create an algorithm in Excel that follows this idea, we can use an exponential function like this:
=8 * (1 – 2^(-0.5 * L4))
Where the initial value for ‘c’ is set at 2.
This formula takes the input value (x in Terry’s original formula and the data in column L on the DSA instrument) and applies the transformation to adjust it to a value out of 8, with higher values being significantly reduced and lower values remaining largely unchanged.
After a bit of fiddling around with the constant to get an appropriate spread of scores in my latest samples of student scores, the final algorithm posted into the DSA is:
=ROUND(8 * (1 – 1.5^(-0.5 * L4)), 0)
With L4 changing in each row to L5, L6, L7, etc. according to the number of students in the rows on the Excel sheet.
This worked perfectly for Terry’s own class and proved equally effective when subsequently used with other classes’ data. It therefore appears that Terry’s contribution does function as a universal conversion algorithm for DSA weighted Quality of Contributions scores to IB assessment criteria scores. I believe that this would also work well to convert the DSA total Speaking and Listening scores to IB English Language Acquistion (ELA) scores. This formula ought to be fairly easy to adapt for other marking schemes too.
Applying a Reliant on Reading Penalty
Following this uncontested solution for the conversion to IB scores, several students remarked that the reliant on reading scores should be penalized using a similar method of reducing high scores whilst protecting lower scores. To this end, I amended column L, which dealt with weighting the scores for low, middle and high quality of contributions to generate a score for understanding and analysis. This column was: =SUM(G4/2, H4*1.5, I4*2) which, as noted above, simply halved the score for low level quality of contributions whilst awarding 1.5 per point for middle and doubling the score for high quality of contributions.
I amended the formula in column L to: =SUM(G4/2, H4*1.5, I4*2) – IF(E4 <= 2, 0, 2^((E4-2)/2))
This retains the original weighting for the quality of contributions but adds a penalty if the student has been reliant on reading more than twice.
By way of explanation, the conditional IF(E4 <= 2, 0, 2^((E4-2)/2)) checks if the score in column E (Reliant on Reading) is 2 or less. If it is, no penalty is applied (i.e. 0 points deducted from the weighted quality of contributions score in DSA column L). For scores higher than 2, however, it uses an exponential function to rapidly increase the penalty.
In this formula, the penalty grows more quickly as the score in column E increases:
- If E4 = 3, the penalty is approximately 1.41
- If E4 = 4, the penalty is approximately 2.00
- If E4 = 5, the penalty is approximately 2.83
This ensures that higher scores in column E result in more severe penalties, which hopefully will further discourage students from just reading material they’ve simply copied from the internet or AI generated. The aim of these discussions is to get the students to respond to each other, not just regurgitate prepared scripts. Besides, due to the unnatural lexical desnity of read responses, these typically do not engage the other students or foster further discussion of the points thus raised.
However, before applying the penalty, we need to ensure that students who genuinely do require that crutch to participate and who are typically struggling to score much are not further penalized or discouraged. Such students need their confidence built, not further dented. This is why the threshold for applying the reliant on reading penalty is set at 2.
In preliminary tests, this seems to be working appropriately.
If you would like to use it, here is the updated DSA instrument with the columns for converting DSA data to an IB MYP assessment score: DSA3-template